VARPA

Calcule la variance sur la base de l'ensemble de la population. Outre des nombres, le calcul peut comprendre du texte et des valeurs logiques telles que VRAI et FAUX.

Syntaxe

VARPA(valeur1;valeur2; ...)

valeur1;valeur2;... représentent 1 à 30 arguments correspondant à une population.

Remarque

La fonction VARPA part de l'hypothèse que les arguments représentent l'ensemble de la population. Si vos données ne représentent qu'un échantillon de cette population, calculez la variance à l'aide de la fonction VARA.
Les arguments contenant la valeur VRAI ont la valeur 1 ; les arguments contenant du texte ou la valeur FAUX ont la valeur 0. Si le calcul ne doit inclure ni texte ni valeur logique, utilisez la fonction VAR.P.
La fonction VARPA utilise la formule suivante :

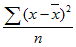
Exemple

Supposons que l'on constitue un échantillon aléatoire des 10 outils estampés par la même machine pendant un cycle de production et que l'on en mesure la résistance à la rupture.

O1	O2	O3	O4	O5	O6	O7	O8	O9	O10	Formule	Description (résultat)
1 345	1 301	1 368	1 322	1 310	1 370	1 318	1 350	1 303	1 299	=VARPA([O1]; [O2]; [O3]; [O4]; [O5]; [O6]; [O7]; [O8]; [O9]; [O10])	Variance des résistances à la rupture pour tous les outils, en supposant que seulement 10 outils sont produits (678,84)